- Institute
- People
- Departments
- Algebra, Geometry and Mathematical Physics (AGMP)
- Branch in Brno (BB)
- Constructive Methods of Mathematical Analysis (CMMA)
- Didactics of Mathematics (DM)
- Evolution Differential Equations (EDE)
- Mathematical Logic, Algebra and Theoretical Computer Science (MLATCS)
- Topology and Functional Analysis (TFA)
- Archive of departments
- Positions
- Research
- Events
- Calendar
- Partnerships
- Links
Noncommutative Geometry and Topology in Prague
Quantum Jet Bundles
Speaker’s name:
Francisco Manuel Castela Simão
Speaker’s affiliation:
Queen Mary University of London
Place:
This talk will take place in the blue seminar room, back building, Žitná 25.
It will also be broadcast on Zoom:
https://cesnet.zoom.us/j/91975183920?pwd=SGdlRUhLS21HUnVFTXBKcE1vYXlrQT09
Meeting ID: 919 7518 3920
Passcode: 102707
It will also be broadcast on Zoom:
https://cesnet.zoom.us/j/91975183920?pwd=SGdlRUhLS21HUnVFTXBKcE1vYXlrQT09
Meeting ID: 919 7518 3920
Passcode: 102707
Date:
Tuesday, 15. November 2022 - 16:00 to 17:00
Abstract:
We formulate a notion of jet bundles over a possibly noncommutative algebra A equipped with a torsion free connection. Among the conditions needed for 3rd-order jets and above is that the connection also be flat and its ‘generalised braiding tensor’ 
obey the Yang-Baxter equation or braid relations. We then build the jet bundle on the graded vector space of symmetric tensors as a braided Hopf algebra 
with of respect to 
. We also cover the case of jet bundles of a given ‘vector bundle’ over A in the form of a bimodule E with flat bimodule connection with its braiding 
obeying the coloured braid relations. Examples include the permutation group 
with its 2-cycles calculus and the 2×2 matrices 
.
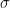obey the Yang-Baxter equation or braid relations. We then build the jet bundle on the graded vector space of symmetric tensors as a braided Hopf algebra with of respect to . We also cover the case of jet bundles of a given ‘vector bundle’ over A in the form of a bimodule E with flat bimodule connection with its braiding obeying the coloured braid relations. Examples include the permutation group with its 2-cycles calculus and the 2×2 matrices .